Some More Pneumatics Revision

Today I set some dates so you know what is coming up homework-wise and NAB-wise. They are:

3/11/11 - Practice NAB in class to include both mechanisms and Pneumatics

7/11/11 - Pneumatics Homework to be handed in 

               (this is in the back of your booklet and should be answered on lined paper)

            - Also if you got less than 31 marks in the Mechanisms homework you need to resubmit this also 

              (remember to come in on Wednesday lunchtime for some extra help)

14/11/11 - Mechanisms and Pneumatics NAB

Today we looked at this circuit and answered the questions below.  Again I will leave the answers as a comment so that you can attempt the questions again first before reading.

Today's Pneumatic Revision

Today we looked at the following pneumatic circuit to check our understanding of pneumatics:

1. Give the full name of all the valves/components.
2. What function do the three highlighted sub-systems perform?
3. Describe the operation of the circuit.
4. If the double acting cylinder has a diameter of 30mm and a rod diameter of 5mm; and the supplied air pressure is 5N/mm, calculate:
      a) The outstroke force
      b) The instroke force

I will leave the answers as a comment so you can have a chance to answer the above questions before seeing them.

Pneumatics

In this topic you need to be able to identify and describe pneumatic circuits and also, as for the NAB, draw these circuits from scratch.

It is therefore very important that you understand how to draw the symbols that you will need to use.

Cylinders:

You can see that the single acting cylinder has one input port which, when air flows in, will outstroke the cylinder.  The spring will make the cylinder instroke as soon as this input air stops.

The double acting cylinder has two input ports, one at each end. This means that air operates the cylinder  for both instroke and outstroke.

Valve Symbols:

The symbols for valves show where external connections (i.e. for main air or exhaust) are connected, as well as the internal connections for each state.

3/2 Valves:

3/2 valves are so called because they have 3 ports and two different states.  The symbol for a 3/2 valve is in two parts to show the two different states it can be in.  The bottom box typically shows the state a valve would be in when just out of the box, or unactuated.   This means that main air is not flowing into the valve, and any excess air in the system can escape out of the exhaust:

The top box is the "action" box.  This is when actuated the valve will allow main air to flow through the valve:

(note, that although I have added main air and exhaust here to help explain, all connections should be drawn on the bottom box.)

To finish your symbol you need to add the actuators.  The actuator make the box they are attached to "happen".  So in this case the push button actuates the valve and allows main air to flow from port 1 to 2.  The spring pushes the top back up again to block off main air when the button is released.

5/2 Valves:

5/2 valves are so called because they have 5 ports and 2 states.  They are primarily used to control a double acting cylinder as main air is always flowing through the 5/2 valve to hold the cylinder outstroke or instroke.  The change of state in a 5/2 valve simply means that main air flows from port 1 > 2 or port 1 > 4, unlike the 3/2 valve which either allowed main air to flow, or blocked it off.

State 1 > 2:

State 1 > 4:

5/2, lever lever valve controlling a double acting cylinder:

Note how all connections are drawn on the left hand box.

Unidirectional Flow Control Restrictors:

A unidirectional FCR combines a bi-directional FCR and a one way valve.  In the diagram below, if the air flows from right to left, it pushes the ball out of the one way valve and air can freely flow along the top of the Unidirectional FCR.  If the air flows from left to right the air pushes the ball into the one way valve which blocks it off and therefore the air is forced to go through the restrictor.

When using a FCR to control the speed of a cylinder it is important to remember to restrict the EXHAUST of the cylinder (the air coming out of the cylinder) so that the cylinder has full pressure air pushing it outstroke and the motion will be smooth with full force.  This is shown below so that the cylinder is being slowed down on outstroke, but will instroke full speed:

Note: just remember that the arrows for the one way valve point away from the cylinder.

Time Delay:


A reservoir can be added after an FCR to cause a time delay.  The air is restricted and therefore takes some time to fill up the reservoir causing the delay. The time can be adjusted by tightening or loosening the FCR or the size of the resistors.

For more information on AND and OR control, and an excellent interactive diagram please look at the BBC Bitesize website here.

Today's Mini Test

Here are the questions and answers for today's mini test:

1. Name and draw the schematic diagram for two mechanisms which transmit motion through 90.

2. Name this mechanism and state its purpose:

Ratchet and Pawl - allows movement in one direction only.

3. Calculate the velocity ratio of this mechanism:

 

4. If the motor in the above system is turning at 500 rev/min, how fast is the output turning?

5. Work out the torque of this motor:

6. Calculate the reaction forces:

7. Name and draw three types of belt which could be used in a belt and pulley system.

8. What could you add to a belt and pulley system which has stretched and become loose?

Tensioner or jockey wheel

Mechanisms

Most of mechanisms was covered last year in S3.  However we have learnt some new things this year:

Velocity Ratio/Linear Speed:
Like last year we had to use Velocity Ratios to work out rotational speed and we looked at how to then find the linear speed of a rope being wound around a drum.
Here are the two examples we looked at in class:

 
VR = 10/40 x 10/15
      = 1/6 (or 0.167)

SPEEDdrum = SPEEDmotor x VR
                     = 500 x 1/6
                     = 83.3 rev/min
                     = 1.39 rev/sec

C = Pi x D
   = 3.14 x 250
   = 785mm
   = 0.785m

SPEEDrope = SPEEDdrum x C
                    = 1.39 x 0.785
                    = 1.09 m/s

VR = 1/2 with 2 ropes

SPEEDload = SPEEDrope x VR
                    = 1.09 x 1/2
                    = 0.55 m/s  

 VR = 10/30 x 10/40
       = 1/12 (or 0.083)

SPEEDdrum = SPEEDmotor x VR
                     = 200 x 1/12
                     = 16.6 rev/min
                     = 0.27 rev/sec

C = π x D
   = 3.14 x 300
   = 942mm
   = 0.942m

SPEEDrope = SPEEDdrum x C
                    = 0.27 x 0.942
                    = 0.254 m/s


Moments:
A moment is the turning effect of a force.  Because a force is being applied to a system, it works like a lever.  So the further away from the pivot the force is applied the greater the moment.  Hence you calculate a moment:

Moment = Force x distance

Moments work on the principle of equilibrium. This means that as the system is not actually moving, all the forces and moments are balanced.  The three laws of equilibrium are:

ΣACM = ΣCWM

ΣFup = ΣFdown

ΣFleft = ΣFdown 

Using these laws we can find out unknown forces or distances.  These are the revision questions we looked at today:

Calculate the reaction forces in the car shown below.

First it might be useful to draw the Free Body diagram to show clearly how the forces are acting on the car.  However you will notice that you are given the mass of the people in the car, not their weight, therefore to find the forces the people will exert on car, you must use W = mg:

F90 = mg              F60 = mg
       = 90 x 9.81          = 60 x 9.81
       = 883N                = 589N

Now that you know the forces, you can start to use the laws of equilibrium.  Make R1 the pivot point so that you can work out R2:

Remember that a moment = force x distance from the pivot.  And you must work out all moments separately, you can't add them without multiplying them by their individual distances first.

  ΣACM = ΣCWM

R2 x 3.5 = (883 x 1) + (589 x 2.5)

    3.5R2 = 883 + 1472.5 

    3.5R2 = 2355.5

         R2 = 673N

 

Now that we know R2, we can use the equal forces law to work out R1.

      ΣFup = ΣFdown

 R1 + R2 = 883 + 589

R1 + 673 = 1472

          R1 = 799N

Then we looked at a car with a caravan on the back.  In this question the tow bar exerts a force both on the car and on the caravan. 

To tackle this question you must consider the car and the caravan separately.  First look at the caravan to work out the force in the tow bar P:

So if R3 is the pivot, you can see that the person is exerting a clockwise force and P an anticlockwise one.

  ΣACWM = ΣCWM

      P x 3.5 = 200 x 1

          3.5P = 200

               P = 57.1N

And using this we only have one unknown in the caravan.  So we can work out R3: 

      ΣFup = ΣFdown

          R3 = 57.1 + 200

               = 257.1N

Now we can work out the forces in the car.  This is the free body diagram for the car:

You will notice that as P is acting up from the car.  This is because there is tension in P and it is being stretched.  The internal forces act to keep P from stretching. So it acts away from both the car and the caravan.
We need to use moments to find the reaction forces.  I would start by making R1 the pivot, so that we can find R2:

                   ΣACWM = ΣCWM

(R2 x 2.5) + (P x 5.5) = 500 x 1
  2.5R2 + (57.1 x 5.5) = 500

               2.5R2 + 314 = 500
                         2.5R2 =  186

                              R2 = 93N

Now we can use the equilibrium in the vertical forces equation to find R1:
      ΣFup = ΣFdown

 R1 + R2 = 500
  R1 + 93 = 500

          R1 = 407N

The next question is slightly easier as it only involves one system, the desk.

Again, the best place to start is by drawing the free body diagram:

Taking moments about R1, we can find R2:

  ΣACWM = ΣCWM

      1 x R2  = (200 x 0.5) + (50 x 1.5)
             R2 = 100 + 75

             R2 =175N

Then using equilibrium in vertical forces we can find R1.
      ΣFup = ΣFdown

 R1 + R2 = 200 + 50
 R1 + 175 = 250

          R1 = 75N

Windlass:
A windlass uses a handle to magnify force.  This can be demonstrated using the Velocity Ratio equation:

Velocity Ratio = Distance moved by effort / Distance moved by load
The distances moved are found by working out the circumference (C = 2π r).  As the handle has a greater circumference you need to put in less force to lift the load when using the windlass.

Torque:

Torque is a turning force, or the turning effect of a force.  This means that when a force is applied to a gear or pulley it is magnified by the distance that force is applied is from the axle, i.e. the radius.  Thus, the bigger the pulley or gear, the bigger the Torque.
Therefore torque can be found using the equation:
         T = Fr
Where T is Torque and is measured in Nm, F is the force, and r is radius.

Power:
Power in mechanical systems are based on P = E/t.  Energy is force x distance and we base our power calculations on revolutions per second so time = 1.  Because this is a turning force we need to know the torque. And the distance is the number of revolutions per second.
Hence mechanical power:  P = 2πNT
P is power measured in W, N is number of turns (rev/s) and T is Torque.

More Energy Practice

Today in the lunchtime drop in session we looked at the transfer of energy from one type to another.

This is the example we used. 

We had to find:
a) The total energy
b) The speed of the man 8m above the ground.

Answer:
a) The man at the top of the building is not moving so all of the energy he possesses is potential. This means that the total energy this man will ever have is equal to the potential energy at the top of the building as shown below.

b) At 8m above the ground the man now has some kinetic energy as he is falling and some potential energy as he is still above the ground.  The total energy the man possesses hasn't changed, only the way the energy is distributed.  Therefore the potential energy and the kinetic energy must add up to the total.  By working out the potential energy the man has a 8m we can then work out the kinetic energy as shown below.  When the kinetic energy is known, the velocity can be found, as shown below. 

Other Notes:
Other things people found confusing was the input energy produced by a fuel like petrol.  Fuel has an energy either per litre or per kg. Therefore the amount of fuel used must be multiplied by the energy stored in the fuel. 
So if petrol has 3.5MJ of energy per kg, and uses 2kg of fuel then the total energy supplied by the fuel is 3.5MJ x 2 = 7MJ.

People also found it difficult to work out which was the input energy and which was the output energy.  The only real rule in trying to work this out is to read the question carefully.  It will explain in the question how the system works.  It may also give you a diagram.  As a rule of thumb a system diagram will read input > process > output.  Therefore a diagram should be drawn in this order.

Other than the above: read the question, highlight and label all the relevant information so that it is clear what you know, and what you are aiming to find out.  Use the data booklet to help you work out what equation you need to use based on what information you have.

Energy Practice NAB

Today we did a practice NAB for your NAB on 27/9/11.  The questions are below and the answers in the pictures at the bottom with the mark allocation drawn on.

Energy Practice NAB

1. A sprung train barrier stops a 2000kg train traveling at 10m/s.  On impact the train exerts a force of 400kN on the barrier.  Calculate the following:
  a) The kinetic energy of the train before it hits the barrier
  b) The compression of the spring in the barrier once the train has stopped moving
  c) The speed of the train once it has collided with the barrier and continued to move after 100mm.

2. An energy audit is carried out on an electrical kettle connected to a 240V supply. The heating element has a resistance of 50Ω and the kettle took 3 minutes to boil 2 litres of water from a starting temperature of 80°c.  Calculate:
  a) The electrical energy going into the kettle
  b) The heat energy produced by the kettle
  c) The energy "lost"
  d) The efficiency of the system

These questions are of the same standard as the NAB, if you are happy with these and how to answer them you will be prepared for the NAB.  Revision of the homework is also a good way to ensure a thorough understanding.  If you were off today at FutureWise then I strongly suggest you come and get your homework marks back!

Here are the answers:

 

Energy Revision

Energy is the ability to do "work".  Which means that it is what makes everything around us happen.  There are different types of energy.  We have been looking at some of the different types of energy and how energy can be transferred from one form to another.  This is a quick revision guide to what we have been doing in class.

Generally energy (or work done) can be found by multiplying the force by the distance it was exerted over, using the equation:
               E (wd) = F d (s)

Power is the rate at which energy is converted. This is another general energy question you need to be aware of. So power is the energy converted over time, or energy is power multiplied by time.
               E = Pt

Potential Energy is the energy a body possesses when it is positioned above the ground (datum) level, it is dependent on the weight (mass x g) x height:
               Ep = mgh

G is the acceleration due to gravity, so the rate at which we are being pulled towards earth.  It is a constant at 9.81 m/s/s on earth.


Kinetic Energy is movement energy.  The greater the mass and speed of a boy, the greater the kinetic energy.
             Ek = 1/2 mv2

Thermal Energy is heat energy.
             Eh = cmΔt 

C is the specific heat capacity of a material and it is constant.  For water C = 4190 J/KgK

Electrical Energy is based on the equations for electrical power, and the general energy power equation.
              E = Pt             P = VI    Therefore  Ee = VIt

Strain energy is the energy generated by stretching or compressing a spring.  First of all you may need to find the force required by multiplying the spring stiffness, in Newtons per millimetre, by the extension or compression.  This will give you the total force to use in the equation:

           Es = 1/2 Fx

Remember that although you need to use millimetres to find the force, x is measured in metres.

To find the efficiency of a system you must look at the energy in and the useful energy out.  Some energy will be "lost" i.e. the heat energy produced by a light bulb, or heat energy produced by friction in moving parts.
            n = Output Energy/Input Energy   (to make it a percentage, multiply by 100.

Today's Energy Mini Test

Here are the answers to today's mini test to help you prepare for the energy NAB.  Numbers in brackets are the marks allocated to each answer/line of working.  Remember that you get marks for working even if the answer is wrong, so make sure that you show clearly the stages you took.

1. State 3 renewable energy sources.
           Choose from geothermal, wind, hydro, solar, tidal/wave        (3)

2.a) Calculate the Spring Stiffness of a spring which was compressed 30mm by a 10N force.
            SS = Force / extension
                 = 0.3N/mm                               (1)

b) Calculate the strain energy of the above spring.
            Es = 1/2 F x                                    (1/2)

                 = 1/2 x 10 x 0.03                       (1/2)

                 = 0.15J                                       (1)

3.a) Calculate the kinetic energy of a ball (mass of 10kg) which is falling, if, at the top of the building it had a potential energy of 12kJ and now has a potential energy of 8kJ.

            Et = Ek + Ep                                   (1/2)

       1200 = Ek + 8000                                (1/2)

           Ek = 4000J (4kJ)                               (1)

b) What height is the ball at now?
           Ep = mgh                                        (1/2)

       8000 = 10 x 9.81 x h                           (1/2)

       8000 = 98.1 x h

            h = 8000/98.1

               = 81.5m                                        (1)

4. What is the acceleration due to gravity (g) on earth?
            9.81 m/s/s                                        (1)     

5. Calculate the speed of a lorry with a weight of 5000N and a kinetic energy of 6500J.
           m = w/g                (1/2)         Ek = 1/2 mv2                (1/2)

               = 5000/9.81      (1/2)      6500 = 1/2 x 510 x v2      (1/2)

               = 510kg              (1)                = 255

                                                           v2 = 6500/255

                                                               = 25.5

                                                           v = 5.05 m/s                   (1)

6. What is the mass of an object which has the potential energy of 7620J at a height of 3m?
         Ep = mgh                        (1/2) 

     7620 = m x 9.81 x 3            (1/2) 

              = m x 29.43

          m = 7620/29.43

              = 260kg                        (1)

7. Calculate the heat energy produced by an electric hair drier if it is 65% efficient and used 240V and 6A over 10 minutes.

     Ee = VIt                                (1/2)       Eh = 0.65 x Ee            (1/2)

          = 240 x 6 x (10 x 600)     (1/2)            = 0.65 x 864000    (1/2)

          = 864kJ                              (1)             = 562kJ                    (1)

Summer Homework

Use the blog and your notes to answer these revision questions.  Make sure you label the questions clearly so it is easy to mark.  ATTEMPT ALL QUESTIONS!  You can always send me a message or write a comment below if you require more help with any of the questions.

Electronics:

1.  Draw a voltage divider which would act as a heat sensor.  Label all the components. Describe how the circuit works, mention temperature, resistance, and voltage.

2. For this transistor circuit, answer the following questions:

 

a)  As the light is on, the transistor must be fully switched on.  State the term used for fully switched on.
b) What is the base-emitter voltage (VBE) of the transistor in this state?
c) The signal from the microprocessor is 5v.  What is the voltage dropped over the base resistor?
d) What, therefore, is the base current which also flows through the base resistor?
e) If the transistor has a current gain (HFE) of 500, what is the current flowing through the lamp? (IC)
f) It is found that 9v is not enough for the lamp to shine it's brightest.  Draw a modified circuit which will allow the transistor circuit to still run on 9v and the lamp to use a new supply voltage of 240v.  Remember to draw all protective components required.  Label all components used.


3. For this motor and light series circuit work out the following:

a) The current in the circuit. (hint: remember P=IV)
b) The resistance of the motor (hint: remember that V=IR)

4. Using the log graphs for the different types of thermistors and the LDR work out the resistance for the following light levels/temperatures:
     a) Type 2 Thermistor at 75 degrees -
     b) Type 5 Thermistor at 60 degrees -
     c) Type 6 Thermistor at 250 degrees -
     d) LDR at 20 lux -
     e) LDR at 2 lux -
     f) LDR at 300 lux -

5. Consider these two circuits:

Circuit B

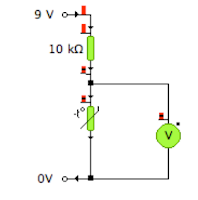Circuit A

 












      a) State the name of this arrangement.
      b) Using the values you found in question 4, find the voltage out of
          circuit A for the following conditions:
           i) Type 2 Thermistor at 75 degrees -
           ii) Type 5 Thermistor at 60 degrees -
           iii) Type 6 Thermistor at 250 degrees -

     c) Using the values you found in question 4, find the voltage out of
         circuit B for the following conditions:
           i) LDR at 20 lux -

           ii) LDR at 2 lux -
           iii) LDR at 300 lux -

     d) For your answers above, if this was the signal to a transistor, state whether
          the transistor would be switched on or off.

Mechanisms

6. Draw a schematic diagram for and label mechanisms which will produce the following types of motion:
     a) Rotary to Rotary motion (two examples)
     b) Rotary to Rotary motion through 90 degrees (two examples)
     c) Rotary to Linear motion (one example)
     d) Rotary to Reciprocating (two examples)

7. State two mechanisms which will allow movement in one direction only/act as a break or safety feature in a system.

8. Consider this compound gear system:

Gear A is a worm gear
Gear B has 24 teeth
Gear C has 12 teeth
Gear D has 24 teeth

    a) Find the velocity ratio
    b) If the motor is turning at 1200rev/min, how fast is gear D turning.
    c) If gear B is turning clockwise, state the direction of gear C and D
    d) Over time the chain becomes loose and it starts to jump over the gears.
        What could be added to the system to ensure that this doesn't happen?


Logic 

9. A burglar alarm should sound if the master switch is on (1) and either a pressure pad next to the door is triggered (1) or the window is opened (0).
   a) Draw the truth table for this system
   b) Write the boolean expression from either your truth table or the English statement
   c) Draw a logic circuit which will fulfill this specification
   d) Suggest a component which could be added to ensure that the alarm
        stays on until reset.  Mark where this should be added with a cross.

10. Draw a block diagram for a system which uses logic to flash a light when it is dark.
      You will need to use: a light sensor, a Pulse Generator, and a lamp.  
                                        Choose the logic gate you will also require.

Pneumatics

11. Draw a 3/2 push button spring return valve. Include main air, exhaust and the port numbers.

12. Add to your question 11 drawing to show how two of these valves (above)
       could be connected to give AND control.

13. Consider this pneumatic circuit:

a) What is the full name of each of the components:
     i) Cylinder A
     ii) Valves B, C, D and E
b) Why are some of the connections dashed and some solid?
c) Describe the operation of the circuit
d) What type of motion does this circuit produce?
e) Draw the two components which could be added to give a delay before the
    cylinder instrokes.  Label them and describe how this works.

14. A double acting cylinder has a diameter of 20mm and a rod diameter of 5mm.
     a) If the air pressure is 4N/mm2 then work out:
         i) The force as the cylinder OUTSTROKES
         ii) The force as the cylinder INSTROKES
     b) Describe, which the use of diagrams, why the force is different on instroke to outstroke.

Homework Answers

Here are the answers to the cover work questions.  If you don't understand anything, scroll down the blog to get more information, or come to ask me at lunchtime or after school.

First of all the simulation task you should have completed in class:

The input of the system is made using a voltage divider with a thermistor and a variable resistor.  Because this is a heat sensor the thermistor must go at the top because as the temperature increases the resistance decreases. As the resistance decreases, less voltage is dropped over the thermistor and therefore a larger share of the supply voltage is dropped over the variable resistor and therefore the signal voltage/voltage out of the voltage divider increases. The base resistor protects the transistor by limiting the current. When the voltage between the base and the emitter of the transistor (VBE) reaches 0.7V the transistor saturates, allowing current to flow from the collector to the emitter and therefore through the lamp, lighting it. The variable resistor is used to adjust sensitivity. Its resistance value could be changed to make the lamp light at different temperatures.  In this case if was adjusted to 1.8k to ensure the lamp would be on above 25.  This could be increased to make the lamp come on at a lower temperature, or decreased to make the lamp light at a higher temperature.

The answers to the theory questions are below:

HOMEWORK DEADLINE

You should complete the 4 past paper questions by:

Monday 27th June

Please be aware that in question 7 d) iii) (tumble drier) it asks for the value of a type 256-051.  This is from an older paper.  Use the type 1 thermistor.

HOMEWORK DEADLINE

You should be working to complete the cover sheets I left you on Friday by:

Tuesday 21st June

This includes a print out of your circuit with a description of how it works, and the answers to the theory questions on the double sided sheet. 

The content of this blog (keep scrolling down!) will help you answer these questions if you are unsure, or come back at lunchtime/after school to ask any questions.

Transistor Circuits - Inputs and Outputs

As mentioned before transistors are used as transducer drivers.

Lets consider some systems.

An automatic street lamp will come on at night when the light level gets too low.
We can draw a systems diagram:

We know how to make a light sensor using a voltage divider with a LDR.
As the light level decreases the resistance of an LDR increases, and so the voltage dropped over it will increase.  This means that there will be a higher voltage signal in the dark if the LDR is at the bottom of the voltage divider.

Using a variable resistor as the top resistor will give you flexibility in the light level required to switch on the lamp.

The signal voltage produced by the light sensor will depend on the light level - this is the signal to the transducer driver (as in the system diagram) so next we have to add the transistor.

We can then lastly add the lamp.

This is how to take a system diagram to a circuit diagram.

Some output transducers need a bigger voltage or current than the transistor/sensing circuit can provide.  For this we need to use a relay - just as we did in the telescope project to make the motor turn because the Alphaboard circuit provided 5V and the motor required 12V.

This page in your notes (P39) shows the relay as a magnetic switch. This means that there is no physical connection between circuits with different power supplies, a magnet pulls a switch closed to complete a higher power circuit.

When a relay switches it creates a large ElectoMagnetic Force (EMF) which creates a very large current.  If this flows back into the transistor it will destroy it and your circuit wouldn't work. Therefore we have to add a diode over the relay to stop the back EMF destroying the transistor.

So our street lamp may require a bigger supply voltage than the sensing circuit.  So we can add a relay in to ensure the lamp lights brightly.

Note the diode.  It protects the transistor from back EMF as the relay switches.

Motors often need greater current/voltage to turn them, so we can use a relay:

This circuit uses a light sensor as its input made using a voltage divider with a LDR at the top and a variable resistor at the bottom.  So as the light level increases the resistance of the LDR will decrease, decreasing the voltage dropped over it, therefore increasing the voltage dropped over the variable resistor and the voltage out of the voltage divider.  When the voltage between the base and emitter (VBE) is 0.7v the transistor will saturate, allowing current to flow from the collector to the emitter, energizing the relay.  This will pull the switch closed in the motor circuit and the motor will turn.

Note that the motor circuit is connected using only one leg of the relay switch, so that when the relay is not energized nothing will happen.

However using the Single Pole double throw relay above only allows the motor to turn in one direction.  We can use a Double Pole Double Throw relay to allow the motor to turn in both directions: one when it is dark and one when it is light: